Clase #3: Definición de Matrices:
Clase #3: Definición de matrices:
Las matrices se utilizan para describir sistemas de ecuaciones lineales, y registrar los datos que dependen de varios parámetros.
Una matriz es una tabla cuadrada o rectangular de datos (llamados elementos) ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales. A una matriz con "m" filas y "n" columnas se le denomina matriz m*n, y a "m" y "n" dimensiones de la matriz.
Tipos de matrices:
Existen varios tipos de matrices en este caso solo explicaremos las siguientes cinco matrices:
Matriz cuadrada: es cuando la matriz tiene el mismo número de filas que de columnas, es decir su dimensión es (n*n).
Matriz diagonal: esta matriz se caracteriza porque todos los elementos que la conforman fuera de la diagonal su valor es 0.
Matriz escalar: la matriz escalar es muy parecida a la matriz diagonal de igual forma sus elementos fuera de la diagonal son equivalentes a 0, pero los elementos que conforman la diagonal son términos iguales.
Matriz unidad: consta de una diagonal en donde los elementos que la forma son iguales a 1, y los que están fuera de la diagonal a 0.
Matriz columna: se le llama así a la matriz que sólo consta de una columna, es decir su dimensión será (m*1).
EJEMPLOS VISTOS EN CLASE:
Suma de matrices:
Resta de matrices:
Multiplicación de un escalar y resta de matrices:
Para las matrices A y B, determine (a) 3A, (b) -B y (c) 3A-B.
Calcular C=AB




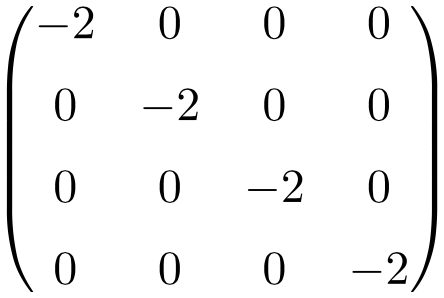
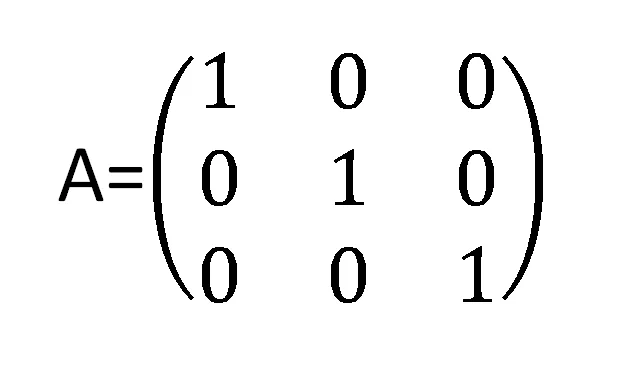






Publicar un comentario
0 Comentarios