Clase #6: Ecuaciones, por el método de Sustitución, Reducción e Igualación:
Clase #6: Ecuaciones, Sustitución-Reducción-Igualación.
1- Método de sustitución: consiste en despejar alguna de las incógnitas en una ecuación (de preferencia la incógnita que tenga menor coeficiente) y sustituir su valor en otra ecuación.
Si tuviéramos un sistema con más de dos incógnitas, la incógnita despejada se sustituye en todas las demás ecuaciones excepto en la que se despejó, y ahora se tendría un sistema, pero con una ecuación y una incógnita menos.
EJEMPLO VISTO EN CLASE:
Paso #1: empezamos despejando el valor de alguna de las dos incógnitas en este caso empezaremos por "x" (valor no final).
Paso #2: elegimos una de las dos ecuaciones iniciales y sustituimos el valor de la letra que despejamos en este caso "x", luego operamos para encontrar el valor de "y".
Paso #3: al tener el valor final de "y", ya podemos encontrar el valor final de "x"; lo hacemos sustituyendo el valor de "y", y operamos para encontrar el valor de "x".2- Método de reducción: también se le conoce como suma o resta de ecuaciones, para poder sumar o restar las ecuaciones y que desaparezca una de las dos incógnitas, los coeficientes deben ser iguales pero de signo distinto. Para ello multiplicamos una de las ecuaciones por el valor contrario del que deseamos eliminar.
EJEMPLO VISTO EN CLASE:
Paso #1: analizamos las ecuaciones y miramos cual letra seria mas fácil de eliminar en este caso eliminamos la letra "y", ¿Cómo lo hacemos? miramos el valor que tiene una de las dos ecuaciones y la otra la multiplicamos por el valor contrario.
Paso #2: en este paso lo único que debemos hacer es sustituir el valor de la letra que despejamos en cualquiera de las ecuaciones.
3- Método de igualación: consiste en despejar la misma incógnita en las dos ecuaciones después igualar los resultados.
EJEMPLO VISTO EN CLASE:
Paso #1: elegimos cualquiera de las dos incógnitas en este caso "x", y la despejamos en ambas ecuaciones.
Paso #2: operamos resultados para encontrar valor de "y".
Paso #3: sustituimos el valor de "y" y operamos.
Paso #4: colocamos respuestas.
Ecuaciones con tres incógnitas por eliminación gaussiana y escalonada.
Paso #1: buscamos los valores mas sencillos de eliminar, en este caso el "x" nos da un nuevo resultado que será nuestros valores ahora.
Paso #2: en las ecuaciones que nos quedaron buscamos la mas fácil de encontrar el valor de alguna incógnita (z), luego vamos sustituyendo valor y así encontramos el valor de cada una.


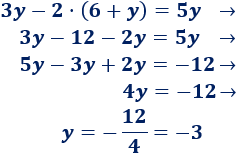





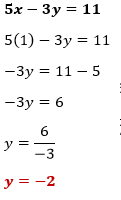









Publicar un comentario
0 Comentarios